Fire – megoldás
2015.04.03. 05:43
Az eredeti feladat itt. Segítség itt.
Megoldás
A tűzijáték helyét szeretnénk megkeresni, azaz az x-tengely egy (p,0) pontját. Rögzített pont súlyát, azaz a sétálandó össztávolságot könnyű kiszámolni N lépésben: minden lakosról konstans időben meghatározhatjuk, hogy ő mennyit gyalogol, majd ezeket összeadjuk. Ezt azonban nem játszhatjuk el az x-tengely összes szóba jövő pontjára, hiszen az négymilliárd pontot jelent, négymilliárdszor N lépésre pedig nincs idő. Ilyenkor hasznos trükk az úgynevezett seprés, jelen esetben vizuálisan úgy képzelhetjük, hogy balról jobbra végigseprünk (ha úgy tetszik, egy függőleges egyenest) a szóba jövő pontokon, magyarul ilyen sorrendben haladunk végig rajtuk. Így tehát elég a súlyváltozást számolnunk, ezáltal megspórolhatjuk, hogy minden alkalommal végigmenjünk az N lakoson.
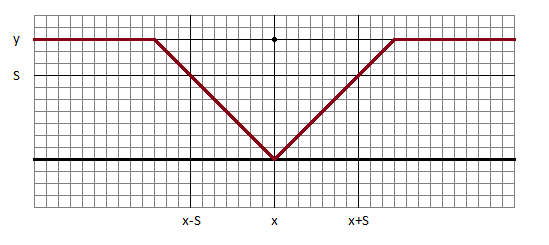
Ehhez persze hatékonyan kell számolni a megváltozást, aminek legegyszerűbb módja, hogy minden koordinátára előre kiszámoljuk a megváltozást. Ez a megváltozás pedig az egyes lakosok által generált megváltozások összege, úgyhogy nézzük meg, hogyan alakul az egy lakos által generált súly, azaz a gyalogolandó távolság. Két eset van, attól függően, hogy S-nél közelebb lakik-e a főúthoz, vagy sem. Legyen (x,y) a pont, ekkor ha y>=S, viszonylag egyszerűen néz ki az ábra (bordóval ábrázolom a sétatávolságot, mint p függvénye, pl. p=x esetén 0):
 Ha viszont y<S, kicsit bonyolódik a dolog:
Ha viszont y<S, kicsit bonyolódik a dolog: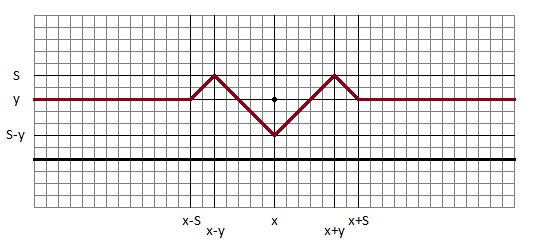 És persze az (x,-y) pontra ugyanazt a grafikont kapjuk, mint (x,y)-ra.
És persze az (x,-y) pontra ugyanazt a grafikont kapjuk, mint (x,y)-ra.
Ezekből a grafikonokból azt egyből láthatjuk, hogy a megoldástervünk így nem fog működni: egy egész intervallumon keresztül folyamatosan változik az adott lakoshoz tartozó súly, ráadásul ez az intervallum nagyon nagy lehet: S és y maximumával arányos. Vagyis ha minden koordinátára el akarnánk tárolni a változást, az legalább SN lépésbe telik, ami túl sok.
Szóval a kedvenceink a szakaszonként konstans függvények, amiket a néhány ugrással könnyen le lehet írni. De azért ezek is elég speciális függvények: szakaszonként lineárisak. Vagyis remekül jellemezhetőek a szakaszok kezdőpontjával és meredekségével! Ráadásul szakaszonként lineáris függvények összege is szakaszonként lineáris, a meredekségek pedig összeadódnak. Márpedig mi az összegnek keressük a minimumát, az pedig könnyen látható, hogy ez a minimum is egy töréspontban lesz. Ezek a töréspontok az érdekes pontok ebben a feladatban. Az adott esetben túl sok összes pont megvizsgálása helyett a viszonylag kevés érdekes pontra való szorítkozás szintén egy gyakori trükk programozási feladatokban.
Minden egyes lakoshoz egy viszonylag kevés (3 vagy 5) törésponttal rendelkező függvény tartozik, ami ráadásul a széleken konstans. Tehát az összegnek is legfeljebb 5N töréspontja lesz, és a széleken az is konstans. Ennyi információ után már nem is nehéz összerakni az O(N log N) algoritmust: minden lakosra eltároljuk a töréspontokat (pontosabban azok x-koordinátáját) és a meredekségváltozást (ami egy egész szám lesz), például a második esetben a következő párokat kapjuk: (x-S,1), (x-y,-2), (x,2), (x+y,-2), (x+S,1). Ezt a legfeljebb 5N párt az x-koordináták szerint lerendezzük, és most már végig is söpörhetünk az érdekes pontokon: A legelső előtt konstans a függvény, ennek értékét könnyen megtalálhatjuk a fenti két eset alapján. Onnantól viszont a meredekséget követjük, ebből pedig pontosan meghatározható, hogy a következő érdekes pontnál mi lesz a függvényérték. Ezen értékek minimumaként pedig megkapjuk a keresett súlyt.
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.