Non-negative Partial Sums – megoldás
2013.02.01. 05:15
Az eredeti feladat itt.
Megoldás
Mindig jó ötlet lerajzolni, hogy mi történik. Ez jelen esetben a részösszegek grafikonját jelenti, azaz az i-edik helyen ábrázoljuk az első i elem összegét. Ha a grafikon végig a nemnegatív tartományban marad, akkor az alap sorozat (vagyis a nulladik elforgatott) egy jó elforgatás. Csakhogy minket nem csak ez érdekel, hanem az összegek bármelyik elemtől kezdve, úgyhogy ne álljunk meg az n-edik összegnél, hanem menjünk körbe még egyszer: az n+i-edik helyen ábrázoljuk az i-edik elemmel (azaz az indexelés szerint ai-1-gyel) megnövelt értékét az n+i-1-edik helyen álló értéknek. Például ha a sorozatunk (1, -2, 0, 3, -1, 2, 1, -2), akkor az ábrázolt értékek sorra 1, -1, -1, 2, 1, 3, 4, 2, 3, 1, 1, 4, 3, 5, 6, 4, ld. ábra.
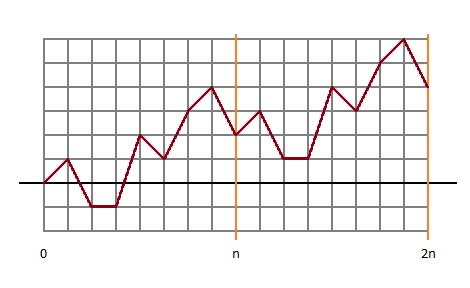 Látható, hogy az i-edik elforgatott (i<n-re) pontosan akkor lesz egy jó sorozat, ha az i-edik érték kisebb (vagy egyenlő), mint az azt követő n-1. Ez egyébként már egy lineáris időben megoldható feladat, de most még jobb dolgunk van. Vegyük észre ugyanis, hogy feltehető, hogy a sorozat elemeinek összege nemnegatív, mert különben semelyik elforgatott sem lesz jó (az összeg mindig az utolsó elem). Ekkor viszont az i-edik érték pontosan akkor kisebb mint a következő n-1, ha az összes későbbinél is kisebb: a minta ugyanaz lesz utána, csak följebb kezdődik. Vagyis mindössze annyi a dolgunk, hogy elindulunk a grafikonon visszafelé, és ha az i-edik helyen (i<n) addig minimális értéket találunk, akkor elkönyveljük, hogy az i-edik elforgatott jó. Ez pedig O(n) futásidőt és memóriát igényel.
Látható, hogy az i-edik elforgatott (i<n-re) pontosan akkor lesz egy jó sorozat, ha az i-edik érték kisebb (vagy egyenlő), mint az azt követő n-1. Ez egyébként már egy lineáris időben megoldható feladat, de most még jobb dolgunk van. Vegyük észre ugyanis, hogy feltehető, hogy a sorozat elemeinek összege nemnegatív, mert különben semelyik elforgatott sem lesz jó (az összeg mindig az utolsó elem). Ekkor viszont az i-edik érték pontosan akkor kisebb mint a következő n-1, ha az összes későbbinél is kisebb: a minta ugyanaz lesz utána, csak följebb kezdődik. Vagyis mindössze annyi a dolgunk, hogy elindulunk a grafikonon visszafelé, és ha az i-edik helyen (i<n) addig minimális értéket találunk, akkor elkönyveljük, hogy az i-edik elforgatott jó. Ez pedig O(n) futásidőt és memóriát igényel.
A fenti példában így három megoldást kapunk: i=2, 3 és 5.
Nekem ez a megoldásom van, ez tűnt természetes útnak, de ha nektek van másik, nyugodtan kommenteljétek ide.
A bejegyzés trackback címe:
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.